

You wouldn't use a list to determine if x is prime. And nobody records large lists of known primes because it is pointless. If nobody recorded that x is prime then I cannot do this). (Given a list of known primes, I can determine whether x is prime or not by checking that it would be in the list if it was prime due to the list size, and then checking whether it is on the list. A number x that has at some point be determined to be a prime is not a "known prime" if it is not recorded.

A "list" of known primes would have to be recorded. If $n$ is composite, it will almost certainly (again, a slippery term) return "COMPOSITE", but there's a small probability $(\frac$ on a large hard drive for say $500, which would pay for some of the cost creating the list. The Miller-Rabin primality test is an algorithm that takes a number $n$, and a "certainty" parameter $m$, and (in layman's terms) if $n$ is prime, it will return "PRIME". Moreover, it's fairly easy to come up with large primes, and it's fairly easy to "guarantee" (guarantee being a slippery term), that a given large number is prime. The size of files in any range will diminish with magnitude, as the frequency of prime numbers decreases.This may be a somewhat unsatisfying answer, but no-one's really keeping a complete list of known primes (to the best of my knowledge). Step 2: Ignore the number 1 and start from 2. *The default of 100,000 means that prime numbers within that range up to the To value will be written to each file. Step 1: First create a list of numbers from 2 to 100 as shown in the figure given below. (For example, 60, 281, 4 means 281 is the 60th prime number and the previous prime is 277.)
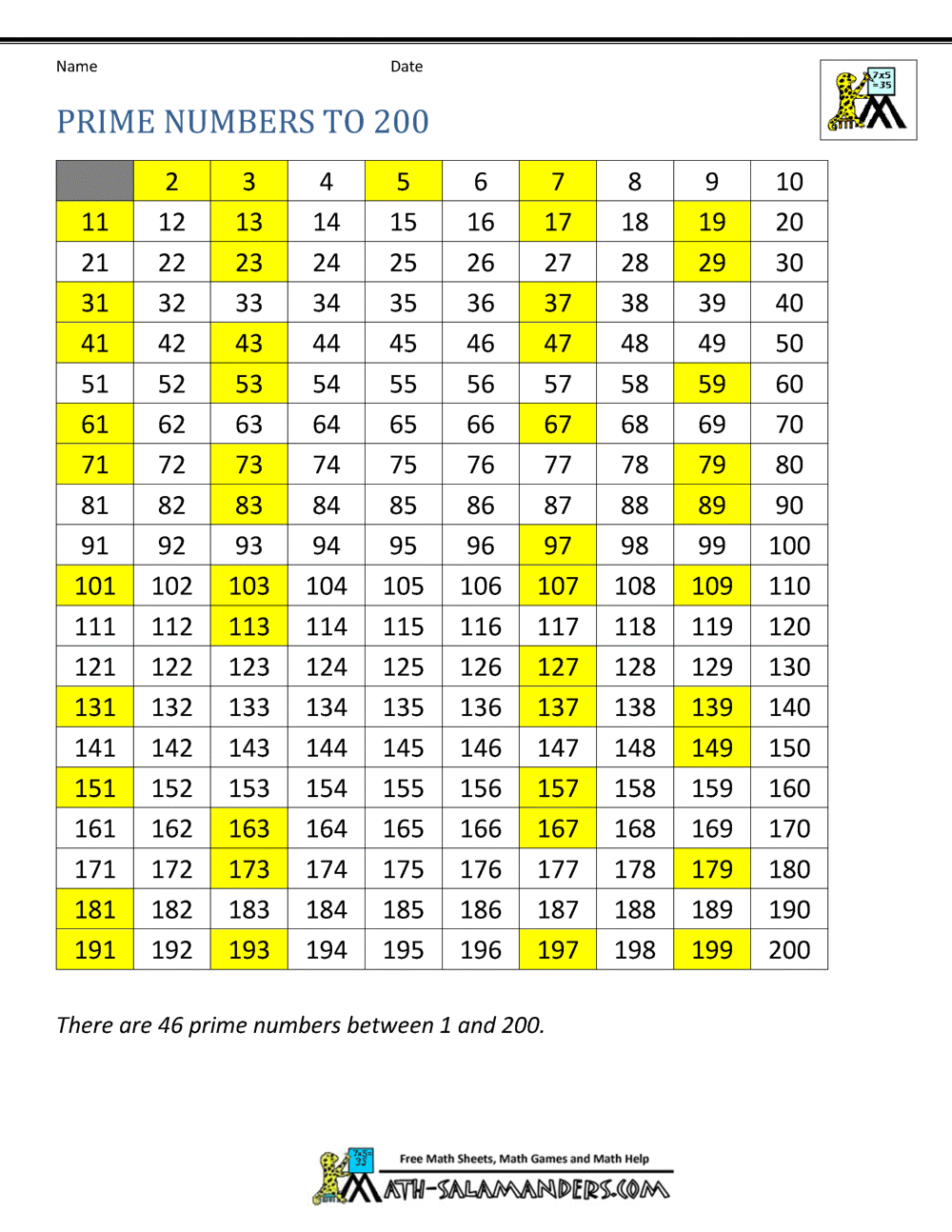

The first number is the sequential rank the second number is the prime the third number is the interval from the previous prime.


 0 kommentar(er)
0 kommentar(er)
